Collision Model for Reaction Rates

Author: John Hutchinson

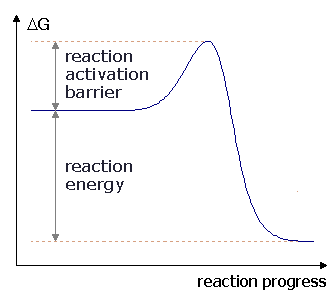
At this point, we have only observed the dependence of reaction rates on concentration of reactants and on temperature, and we have fit these data to equations called rate laws. Although this is very convenient, it does not provide us insight into why a particular reaction has a specific rate law or why the temperature dependence should obey equation 17. Nor does it provide any physical insights into the order of the reaction or the meaning of the constants a and b in equation 17.

We begin by asking why the reaction rate should depend on the concentration of the reactants. To answer this, we consider a simple reaction between two molecules in which atoms are transferred between the molecules during the reaction. For example, a reaction important in the decomposition of ozone O₃ by aerosols is

O₃(g)+Cl(g) O₂(g)+ClO(g)

The rate of collisions depends on the concentrations of the reactants, since the more molecules there are in a confined space, the more likely they are to run into each other. To write this relationship in an equation, we can think in terms of probability, and we consider the reaction above. The probability for an O₃ molecule to be near a specific point increases with the number of O₃ molecules, and therefore increases with the concentration of O₃ molecules. The probability for a Cl atom to be near that specific point is also proportional to the concentration of Cl atoms. Therefore, the probability for an O₃ molecule and a Cl atom to be in close proximity to the same specific point at the same time is proportional to the [O₃] times [Cl].

It is important to remember that not all collisions between O₃ molecules and Cl atoms will result in a reaction. There are other factors to consider including how the molecules approach one another. The atoms may not be positioned properly to exchange between molecules, in which case the molecules will simply bounce off of one another without reacting. For example, if the Cl atom approaches the center O atom of the O₃ molecule, that O atom will not transfer. Another factor is energy associated with the reaction. Clearly, though, a collision must occur for the reaction to occur, and therefore there rate of the reaction can be no faster than the rate of collisions between the reactant molecules.

Therefore, we can say that, in a bimolecular reaction, where two molecules collide and react, the rate of the reaction will be proportional to the product of the concentrations of the reactants. For the reaction of O₃ with Cl, the rate must therefore be proportional to [O₃][Cl], and we observe this in the experimental rate law in table 4. Thus, it appears that we can understand the rate law by understanding the collisions which must occur for the reaction to take place.

We also need our model to account for the temperature dependence of the rate constant. As noted at the end of the last section, the temperature dependence of the rate constant in equation 17 is the same as the temperature dependence of the equilibrium constant for an endothermic reaction. This suggests that the temperature dependence is due to an energetic factor required for the reaction to occur. However, we find experimentally that equation 17 describes the rate constant temperature dependence regardless of whether the reaction is endothermic or exothermic. Therefore, whatever the energetic factor is that is required for the reaction to occur, it is not just the endothermicity of the reaction. It must be that all reactions, regardless of the overall change in energy, require energy to occur.

A model to account for this is the concept of activation energy. For a reaction to occur, at least some bonds in the reactant molecule must be broken, so that atoms can rearrange and new bonds can be created. At the time of collision, bonds are stretched and broken as new bonds are made. Breaking these bonds and rearranging the atoms during the collision requires the input of energy. The minimum amount of energy required for the reaction to occur is called the activation energy, Ea. This is illustrated in figure 8, showing conceptually how the energy of the reactants varies as the reaction proceeds. In subfigure 8.1, the energy is low early in the reaction, when the molecules are still arranged as reactants. As the molecules approach and begin to rearrange, the energy rises sharply, rising to a maximum in the middle of the reaction. This sharp rise in energy is the activation energy, as illustrated. After the middle of the reaction has passed and the molecules are arranged more as products than reactants, the energy begins to fall again. However, the energy does not fall to its original value, so this is an endothermic reaction.

Subfigure 8.2 shows the analogous situation for an exothermic reaction. Again, as the reactants approach one another, the energy rises as the atoms begin to rearrange. At the middle of the collision, the energy maximizes and then falls as the product molecules form. In an exothermic reaction, the product energy is lower than the reactant energy.

Figure 8 thus shows that an energy barrier must be surmounted for the reaction to occur, regardless of whether the energy of the products is greater than (subfigure 8.1) or less than (subfigure 8.2) the energy of the reactants. This barrier accounts for the temperature dependence of the reaction rate. We know from the kinetic molecular theory that as temperature increases the average energy of the molecules in a sample increases. Therefore, as temperature increases, the fraction of molecules with sufficient energy to surmount the reaction activation barrier increases.

Figure 8.1: Reaction Energy. Endothermic Reaction	Figure 8.2: Reaction Energy. Exothermic Reaction

Although we will not show it here, kinetic molecular theory shows that the fraction of molecules with energy greater than E_α at temperature T is proportional to e^-(Eα/RT). This means that the reaction rate and therefore also the rate constant must be proportional to e^-(Eα/RT). Therefore we can write

k(T) = Ae-(Eα/RT)

[18]

where A is a proportionality constant. If we take the logarithm of both sides of equation 18, we find that

ln(k(T)) = -(Eα/RT) + lnA

[19]

This equation matches the experimentally observed equation 17. We recall that a graph of ln(k) versus 1/T is observed to be linear. Now we can see that the slope of that graph is equal to -Eα/R.

As a final note on equation 19, the constant A must have some physical significant. We have accounted for the probability of collision between two molecules and we have accounted for the energetic requirement for a successful reactive collision. We have not accounted for the probability that a collision will have the appropriate orientation of reactant molecules during the collision. Moreover, not every collision which occurs with proper orientation and sufficient energy will actually result in a reaction. There are other random factors relating to the internal structure of each molecule at the instant of collision. The factor A takes account for all of these factors, and is essentially the probability that a collision with sufficient energy for reaction will indeed lead to reaction. A is commonly called the frequency factor.