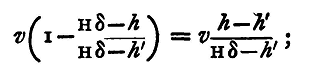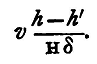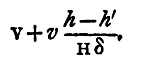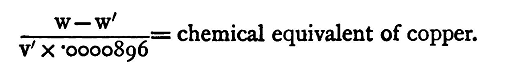Faraday's Law

The electro-chemical equivalent of an element or radicle in absolute measure is the number of units of mass of the element or radicle separated from one of Its compounds by the passage of an absolute unit of electricity.

The ratio of the electro-chemical equivalents of two elements may thus be found by determining the mass of each element deposited by the same quantity of electricity. In order to ensure that the same quantity of electricity passes through two solutions we have only to include both in one circuit with a battery. This plan is to be adopted in the following experiment to compare the electro-chemical equivalents of hydrogen and copper.

Arrange in circuit with a battery (fig. 59) (the number of cells of which must be estimated from the resistance⁽¹⁾ to be overcome, and must be adjusted so as to give a supply of bubbles in the water voltameter that will form a measurable amount of gas in one hour) (1) a beaker U of copper sulphate, in which dip two plates of copper C, C', soldered to copper wires passing through a piece of wood which acts as a support on top of the beaker, and (2) a water voltameter⁽²⁾ V. Mount over the platinum plate P', by which the current is to leave the voltameter, a burette to be used for measuring the amount of hydrogen generated during the experiment, taking care that all the hydrogen must pass into the burette. Place a key in the circuit, so that the battery may be thrown in or out of circuit at will.

The zinc of the battery must be in connection with the plate C' on which copper is to be deposited. The copper or platinum is in connection with the platinum plate P, on which oxygen will be deposited.

About three Grove's cells will probably be required for a supply of gas that can be measured in a convenient time; and as this will correspond to a comparatively large current, the plates of copper should be large, say 6 in. x 3 in., or the deposit of copper will be flocculent and fall off the plate.

When the battery has been properly adjusted to give a current of the right magnitude, the apparatus will be in a condition for commencing the measurements. Accordingly, take out, dry, and carefully weigh the copper plate on which the metal will be deposited during the experiment. This of course is the plate which is connected with the negative pole of the battery. Let its weight be w.

After weighing the copper plate no current must be sent through the voltameter containing it, except that one which is to give the required measurement.

Read the position of the water in the burette - the height in centimetres of the water in the burette above the level of the water in the voltameter. Let this be h. Read the barometer; let the height be H. Read also a thermometer in the voltameter; let the temperature be t°C. Make the battery circuit by closing the key and allow the current to pass until about twenty centimetres of the burette have been filled by the rising gas. Shut off the current, and dry and weigh the same plate of copper again; let the weight be w'.

Then the amount of copper deposited by the current is w'-w.

Read again the position of the water in the burette. From the difference between this and the previous reading we may obtain the volume of the gas generated. Let the difference in volume actually observed be v cubic centimetres, and let the height of the water in the burette above that in the voltameter at the end of the experiment be h'.

Before using v to find the mass of hydrogen deposited we have to apply several corrections.

There was some gas above the water in the burette before the experiment began. The pressure of the gas above the water has been increased by the experiment, and this gas has in consequence decreased in volume. We require to find what the decrease is.

Let the original volume of the gas be v. The graduations on the burette are generally not carried to the end, and to find v we require to know the volume between the last graduation and the tap of the burette. For this purpose a second burette is needed. This is filled with water to a known height. The burette to be used in the experiment is taken and inverted, being empty. Water is run into it from the second burette until it is filled up to the first graduation; the quantity of water so run in is found by observing how far the level in the second burette has fallen. Or, if it be more convenient, the method may be reversed; the second burette being partly filled as before, the first burette is also filled up to some known graduation, and all the water which it contains is run out into the second; the rise in level in this gives the quantity of water which has run out, and from this we can find the volume required between the bottom of the burette and the first graduation; knowing this we find the volume v easily.

Now this gas of volume v was at the commencement under a pressure equal to the difference between the atmospheric pressure and the pressure due to a column of water of height h; if δ be the specific gravity of mercury, the pressure due to a column of water of height h is the same as that due to a column of mercury of height h/δ; so that H being the height of the barometer, the pressure of the gas will be measured by the weight of a column of mercury of height H - h/δ, while at the end of the experiment the pressure is that due to a column H - h'/δ. Therefore the volume which the gas now occupies is

so that the decrease required is

and h' being small compared with Hδ, we may write this:

This must be added in the observed volume V to find the volume occupied by the gas electrolysed, at a pressure due to a column of mercury of height H-h'/δ, giving us thus as the volume,

It is sometimes more convenient to avoid the necessity for this correction by filling the burette with water before beginning, so that v, the space, initially filled with gas is zero. If this plan be adopted we shall still require to know the volume between the end of the burette and the graduations, and this must be obtained as described above.

Correction for aqueous vapour. - The solution of sulphuric acid used in the voltameter is exceedingly dilute, and it may be supposed without error that the hydrogen gas comes off saturated with aqueous vapour; the pressure of this vapour can be found from the table (34), for the temperature of the observation, t°C. Let it be e. Then if e be expressed as due to a column of mercury of e centimetres in height, the pressure of the hydrogen will be measured by

and its volume at this pressure and temperature t is

Thus its volume at a pressure due to 76 centimetres and temperature 0°C. is

Let this be v'. The weight required is v'*0.0000896g, 0.0000896 being the density of hydrogen.

But according to Faraday's fundamental law of electrolysis, the weights of two elements deposited by the same current in the same time are proportional to their chemical equivalents. We must, therefore, have

The value of the equivalent, as deduced from chemical experiments, is 31.75.

Experiment.

Determine by the use of voltameters the chemical equivalent of copper.

(1)	Sec p. 421.
(2)	An arrangement which is easily put together is shown in the figure. The plate P' is inside a porous pot, such as is used in a Leclanché battery, and the open end of the burette is sealed into the top of the pot by means of pitch or some kind of insulating cement. The hydrogen is formed inside the pot and rises into the burette. A graduated Hofmann voltameter is of course better, but the above can be made in any laboratory with materials which are always at hand.