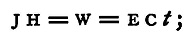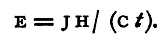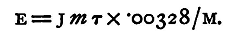Joule's Law - Measurement of Electromotive Force

We have seen that work is done when a quantity of electricity passes from a point at one potential to a second point at a different one. If Q be the quantity of electricity which passes thus, and E the difference of potential, or electromotive force, maintained constant between the points while Q passes, then the work done is Q x E. If the electricity pass as a steady current of strength C, for a time t seconds, then, since the strength of a current is measured by the quantity which flows in a unit of time, we have Q = ct, and if W be the work done,

If this current flow in a wire the wire becomes heated, and the amount of heat produced measures the work done, for the work which the electricity does in passing from the point at high to that at low potential is transformed into heat. If H be the amount of heat produced and J the mechanical equivalent of heat, that is, the number of units of work which are equivalent to one unit of heat, then the work required to produce H units of heat is JH. Hence we have

whence

Now J is a known constant, H can be measured by immersing the wire in a calorimeter (see §39) and noting the rise of temperature of a weighed quantity of water which is contained therein; if a copper-voltameter be included in the circuit Ct is obtained, knowing the electro-chemical equivalent of copper, by determining the increase in weight of the cathode. We can thus find E, the difference of potential between the two points at which the current respectively enters and leaves the wire in the calorimeter. For the calorimeter we use a small vessel of thin sheet copper polished on the outside and suspended in another copper vessel, as in §39. The water equivalent of this must be determined, as is explained in that section, either experimentally or by calculation from the weight of the vessel and the known specific heat of copper, which for this purpose may be taken as 0.1.

A small stirrer made of thin copper wire coiled into a spiral may be included in the estimate with the calorimeter determination. The outer vessel of the calorimeter is closed by a copper lid with a hole in the middle, through which a cork passes. The end of the stirrer passes through a hole in this cork, and through two other holes pass two stout copper wires, to the ends of which the wire to be experimented on is soldered. The thermometer is inserted through a fourth hole. The bulb of the thermometer should be small, and the stem should be divided to read to tenths of a degree. The wire should be of German-silver covered with silk and coiled into a spiral. Its length and thickness will depend on the nature of the source of electromotive force used. If we take a battery of three Grove's cells of the usual pint size, it will be found that the electrical resistance of the wire (see chap, xx.) should be about 4 ohms. The two ends are soldered on to the copper electrodes and the wire completely immersed in the water of the calorimeter. It must be carefully remembered that the quantity which we are to determine is the difference of potential between the two points at which the wire cuts the surface of the water.

Some of the heat developed in the wire will of course remain in it, and in our calculations we ought strictly to allow for this. It will be found, however, that in most instances the correction is extremely small, and may, for the purposes of the present experiment, be safely neglected We may assume that the whole of the heat produced goes into the water and the calorimeter. But the experiment lasts for some time, and meanwhile the temperature of the calorimeter is raised above that of the surrounding space, so that heat is lost by radiation. We shall show how to take the observations so as to compensate for this.

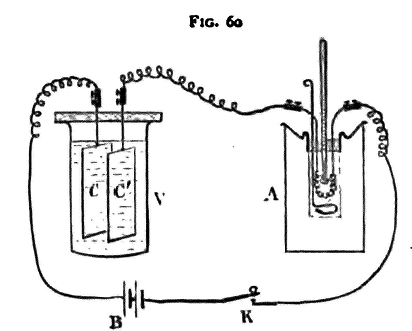
The apparatus is arranged as follows (fig. 60): The cathode C of the voltameter V is carefully weighed and connected to the negative pole of the battery B, the anode C' being connected by means of a piece of copper wire with one of the ends of the wire in the calorimeter A; the other end of this wire is joined through a key K to the positive pole of the battery.

The plates of the voltameter must be so large and so close together that its resistance maybe very small indeed compared with that of the wire in the calorimeter: otherwise the rise of temperature in the calorimeter may be hardly large enough for convenient measurement without using a considerable number of battery cells.

To perform the experiment, note the temperature of the water and allow the current to flow, keeping the water well stirred; the temperature will gradually rise. After two minutes stop the current; the temperature may still rise slightly, but if he stirring has been kept up, the rise, after the current has ceased flowing, will be very small. Let the total rise observed be τ₁ degrees. Keep the circuit broken for two minutes; the temperature will probably fall. Let the fall be τ₂ degrees. This fall during the second two minutes is due to loss of heat by radiation; and since during the first two minutes the temperature did not differ greatly from that during the second two, we may suppose that the loss during the first two minutes was approximately the same as that during the second two; so that, but for this loss, the rise of temperature during those first two minutes would have been τ₁+τ₂ degrees.

We thus find the total rise of temperature produced in the mass of water in two minutes by the given current by adding together the rise of temperature during the first two minutes and the fall during the second two minutes. Take six observations of this kind, and let the total rise of temperature calculated in the manner above described be τ degrees; let the mass of water, allowing for the water equivalent of the calorimeter and stirrer, be m grammes, then the quantity of heat given out by the current in twelve minutes is mτ units.

Let M grammes of copper be deposited by the same current; then since the passage of a unit of electricity causes the deposition of 0.00328 gramme of copper, the total quantity of electricity which has been transferred is M/0.00328 units, and this is equal to Ct in the equation for E. Hence

Now the value of J in C.G.S. units is 42*10⁶, so that we have

The value of E thus obtained will be given in C.G.S. units; the practical unit of E.M.F. is called a volt, and one volt contains 10⁸ C.G.S. units; hence the value of E in volts is

We have used the results of the experiment to find E. If, however, E can be found by other means - and we shall see shortly how this may be done - the original equation, JH = ECt, may be used to find J or C. It was first employed by Joule for the former of the two purposes, i.e. to calculate the mechanical equivalent of heat, and the law expressed by the equation is known as Joule's law.

Experiment. - Determine the difference of potential between the two ends of the given wire through which a current is flowing.

Enter results thus: