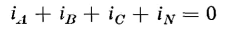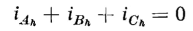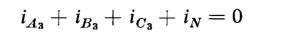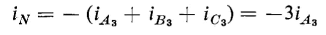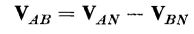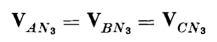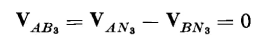Third Harmonics in 3-Phase Transformer Operation

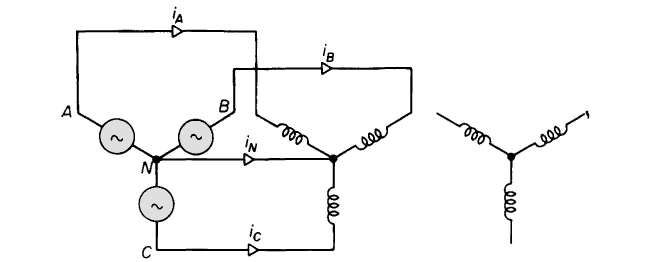
It was shown in Section 5-3 that the sinusoidal flux in iron cores requires a third-harmonic component in the exciting current, which, although small in relation to the rated current, may produce undesirable effects in 3-phase transformer operation.

Consider three identical unloaded, single-phase transformers connected wye-wye to a 3-phase generator with their primary neutral connected to the generator neutral as shown in Fig. 6-32. The sum of the instantaneous currents flowing in the primary must equal zero, i.e.

[6-94]

The fundamental components, as well as harmonics - not including the third and multiples thereof, are 120° apart, and, being of equal amplitudes, their sum is

[6-95]

where the subscript h stands for the order of the harmonics 1, 5, 7, 11, but not for 3, 9, 15, etc. It should be remembered that harmonics in the exciting current of an iron-core transformer are odd for sinusoidal flux when there is no d-c component of flux. It follows from Eqs. 6-94 and 6-95 that the neutral current in the unloaded transformers, or in such as deliver balanced sinusoidal 3-phase currents, is comprised of third-harmonic current, which is the sum of the third harmonics in the three phases, thus

or

[6-96]

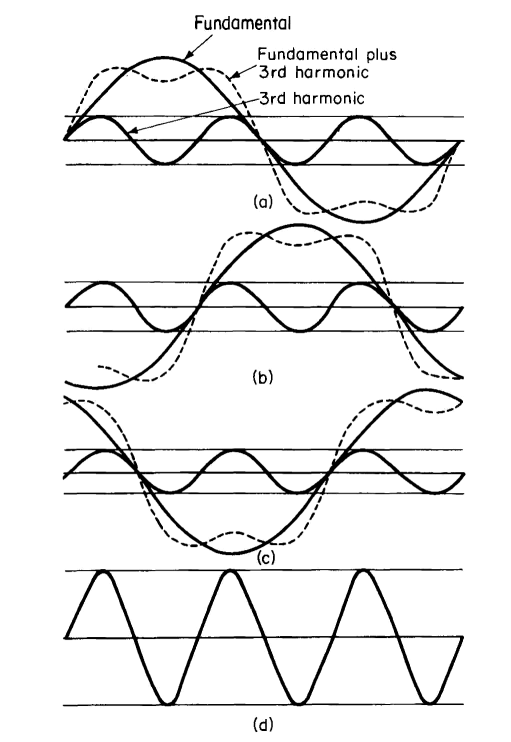
Figures 6-33(a), 6-33(b), and 6-33(c) show balanced 3-phase waves that are comprised of a fundamental and a third harmonic. The sum of the three

Figure 6-32. Exciting currents and neutral current in wye-wye transformer connection.

Figure 6-33. Balanced 3-phase waves containing a fundamental and a third harmonic component, (d) Sum of the three waves of (a), (b), and (c).

balanced waves is shown in Fig. 6-33(d) and is a pure third harmonic having an amplitude equal to three times that of the third harmonic in any one phase.

If the neutral connection between the transformer primaries and the generator is broken, then the path for the third-harmonic currents is interrupted and the third harmonics in the exciting current will be suppressed. As a result, the flux cannot be sinusoidal, as it will contain a third harmonic, which in turn produces a third harmonic in the transformer voltages. These third harmonics show up only in the line-to-neutral voltage if the transformers are identical, and will not appear in the line-to-line voltages because the line-to-line voltages are the phasor difference between the line-to-neutral voltages, i.e.

The third harmonics in the line-to-neutral voltages of all three phases are equal and in phase with each other and, therefore, cancel in the line-to-line

Figure 6-34. Third-harmonic voltage across an open corner in the delta on the secondary of a wye-delta connection with the primary neutral isolated.

voltages. This becomes evident when the difference is taken between any two of three waves a, b, and c of Fig. 6-33. Since

and

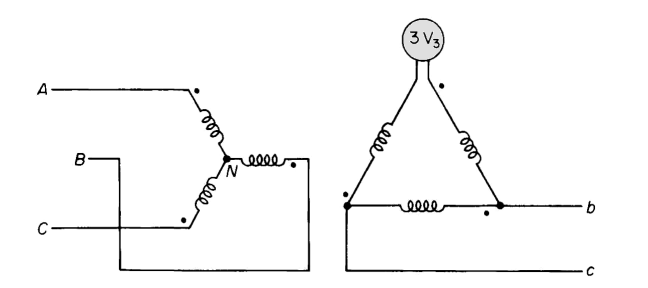
When the primaries are connected in delta, the third-harmonic components in the current are free to flow, but will not show up in the line currents because the line currents are the differences between the currents flowing in the delta as shown in Fig. 6-21. The delta connection on the secondary side of a wye-delta arrangement also provides a path for the third-harmonic components in the exciting mmf. Figure 6-34 shows the primaries of a wye-delta arrangement connected in wye with the neutral isolated. One corner of the delta is shown open. Since the neutral is isolated, there is no return path on the primary side for the third harmonics in the exciting current, causing third harmonics to appear in the voltage across each primary winding. There will be corresponding third harmonics in the voltages across each secondary winding if one or more corners of the delta are open. The voltage appearing across the open corner of the delta in Fig. 6-34 is the sum of the voltages in the three secondary windings, and, if the exciting characteristics of the three phases are identical, the sum of the fundamentals, as well as that of all harmonics - except the third and its multiples - will be zero since these are all equal and 120° apart. The multiples of the third harmonics are usually negligible. The third harmonics are equal and in phase with each other. And the voltage across the open corner of the delta is three times the third-harmonic voltage in one phase of the secondary. Thus, if V₃ is the third harmonic voltage per phase in the delta, then 3V₃ is the voltage across the open corner of the delta.

Closing the open corner of the delta in Fig. 6-34, for normal operation, short circuits the third-harmonic emf 3 V₃, causing a third-harmonic current to circulate in the delta, thus producing a substantially sinusoidal flux. If, in addition, the primary neutral is closed, the third-harmonic components of the mmf required by the sinusoidal flux divide between the primary and secondary, depending upon their relative third-harmonic leakage impedances.

Since the delta connection provides a path for the third-harmonic current, and because it assures balanced voltages, most 3-phase transformations include a delta winding, which makes the wye-delta or delta-wye arrangement very common. Where wye-wye transformation is required, it is quite common to incorporate a third winding, known as a tertiary, connected in delta. Generally, the rating of the delta-connected tertiary is considerably lower than that of the primary and secondary wye-connected windings.