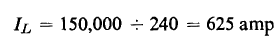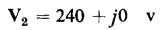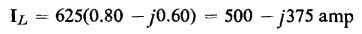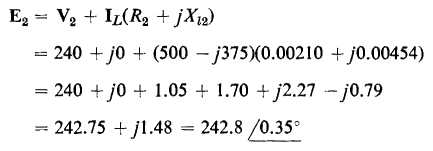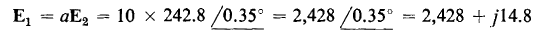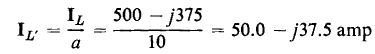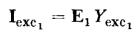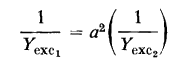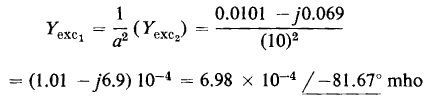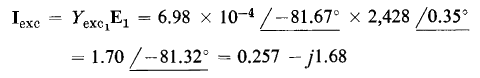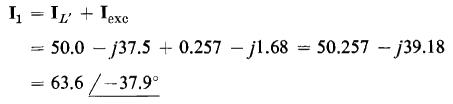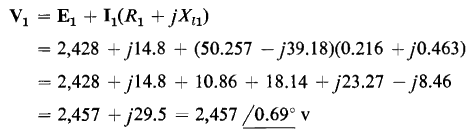Capacitors, Magnetic Circuits, and Transformers is a free introductory textbook on the physics of capacitors, coils, and transformers. See the editorial for more information....

Home The Transformer Equivalent Circuit of the Transformer The Exact Equivalent Circuit
 
del.icio.us Reddit Facebook StumbleUpon MySpace Twitter Search the VIAS Library  |  Index

The Exact Equivalent Circuit

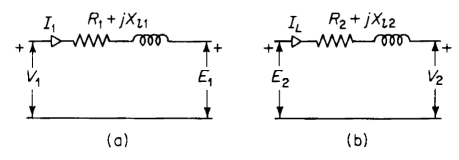
Figure 6-6(a) shows the equivalent circuit of an ideal transformer modified to take into account the exciting current of an iron-core transformer. Equations 6-44 and 6-45 suggest further modifications of the ideal transformer

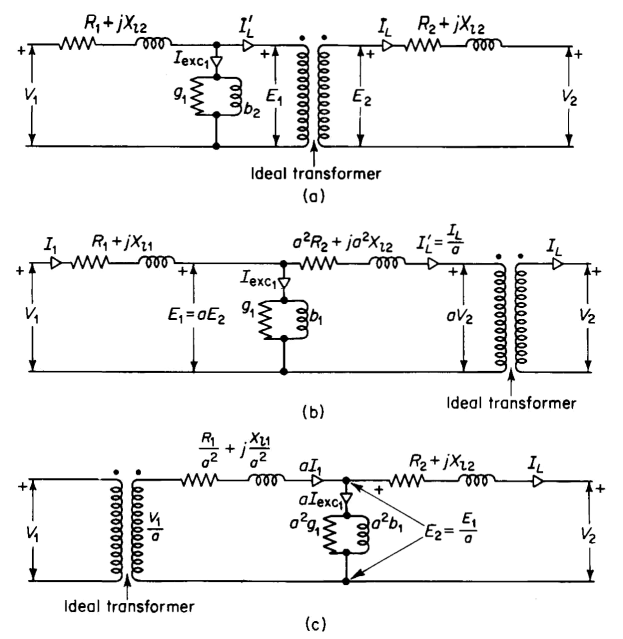
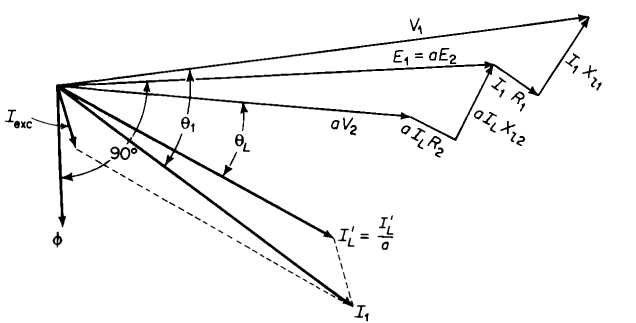
Figure 6-10. Equivalent circuits of (a) primary leakage impedance (Eq. 6-44), and (b) secondary leakage impedance (Eq. 6-45).

by taking into account the effect of the resistance and leakage reactance of the windings. Equation 6-44 and 6-45 are satisfied by the relationships shown in the equivalent circuits of Figs. 6-10(a) and 6-10(b) respectively. The equivalent circuit that completely represents an iron-core transformer in which capacitance effects are negligible and in which the leakage inductances are linear combines the circuits of Figs. 6-10(a) and 6-10(b) with that of Fig. 6-6(a) as shown in Fig. 6-11.

A phasor diagram based on the exact equivalent circuit of Fig. 6-11(b) is shown in Fig. 6-12. In this phasor diagram θL is the power factor angle of the load connected to the secondary terminals of the transformer. Also, the flux is shown lagging the induced emf by an angle of 90° in accordance with the phasor diagram of Fig. 5-9.

Figure 6-11. Exact equivalent circuits of a transformer.
Figure 6-12. Phasor diagram for exact equivalent circuit [Figure 6-11(b)].

 

Example 6-2: The constants of a 150-kva, 2400/240-v, 60-cps transformer are as follows

Resistance of the 2400-v winding R1 = 0.216 ohm
Resistance of the 240-v winding R2 = 0.00210 ohm Leakage reactance of the 2400-v winding Xl1 = 0.463 ohm
Leakage reactance of the 240-v winding Xl2 = 0.00454 ohm
Exciting admittance on the 240-v side yexc = 0.0101 - j0.069 mho

(a) Draw the equivalent circuit on the basis of Fig. 6-11 (a) showing the numerical values of the leakage impedances and the exciting admittance expressed in complex form.

Figure 6-13. Equivalent circuit for transformer of Example 6-2.

(b) Determine the values of the emfs E1 and E2 induced by the equivalent mutual flux, the exciting current Iexc, the primary current I1 at 0.80 power factor, current lagging, and the applied primary voltage when the transformer delivers rated load at rated secondary voltage.

 
Solution: (a) The equivalent circuit is shown in Fig. 6-13.

(b) The rated secondary terminal voltage is 240 v and the rated load (rated output) of the transformer is 150000 va at 240 v. The rated load current is therefore

Let the phasor that represents the secondary terminal voltage V2 lie on the axis of reals as shown in Fig. 6-12, then

and the load current expressed as a phasor is

The secondary induced voltage E2 in Fig. 6-12 must equal the phasor sum of the secondary terminal voltage plus the voltage drop across the secondary leakage impedance, thus

Since the primary induced voltage E1 and the secondary induced voltage E2 are both produced by the mutual flux, their ratio E1/E2 must equal the turns ratio a = N1/N2 = 10, and we have

The load component IL' of the primary current expressed in phasor form is

The primary current is the phasor sum of the load component IL' and the exciting current Iexc. The exciting current produces the mutual flux, so to speak, and is obtained by multiplying the primary induced voltage by the exciting admittance referred to the primary side, i.e.

The value of the admittance in the given data is as measured on the secondary side. This admittance is referred to the primary side by making use of the impedance ratio a2. It should be remembered that an impedance is transferred from the secondary side to the primary side of a transformer by multiplying its value by the impedance ratio. Further, impedance is the reciprocal of admittance, and on transferring the exciting admittance from the secondary to the primary side, we have

or

The primary exciting current is therefore

From Fig. 6-12 it is evident that the primary current is

The primary applied voltage is the sum of the primary induced voltage and the voltage drop across the primary leakage impedance. Hence,

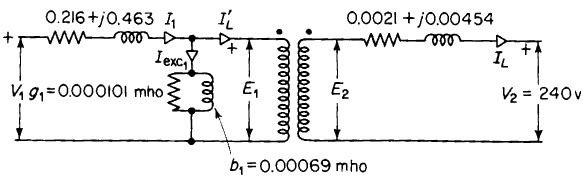
All three of the equivalent circuits shown in Fig. 6-11 lead to exactly the same values of primary current, I1, and primary applied voltage, V1 as were obtained in the solution of Example 6-2.

Home The Transformer Equivalent Circuit of the Transformer The Exact Equivalent Circuit

Last Update: 2011-01-15