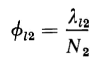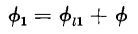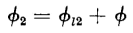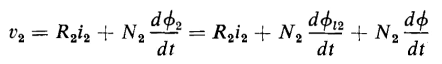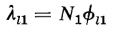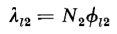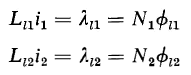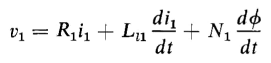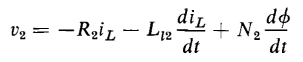Leakage Flux and Leakage Reactance

It was pointed out in Section 6-3 that in an actual iron-core transformer all the magnetic flux is not confined completely to the core, especially under load conditions, i.e., when the secondary is delivering appreciable current. Although Eqs. 6-7 and 6-8 could theoretically be made to take into account the mutual flux and the leakage fluxes to give the total induced emf in each

Figure 6-8. Winding arrangement in shell-type transformer showing approximate paths taken by mutual flux and primary and secondary leakage fluxes.

of the two windings, it is more convenient to divide the magnetic flux into three components. These are

• The mutual flux Φ, which is confined almost completely to the core and which is common to both the primary and the secondary windings. This flux transforms the power from primary to secondary and is due to the resultant mmf of the primary and secondary windings.
• The primary leakage flux Φ_l1, due to the mmf of the primary winding and which links the primary without linking the secondary.
• The secondary leakage flux Φ_l2, due to the mmf of the secondary winding and which links the secondary without linking the primary winding.

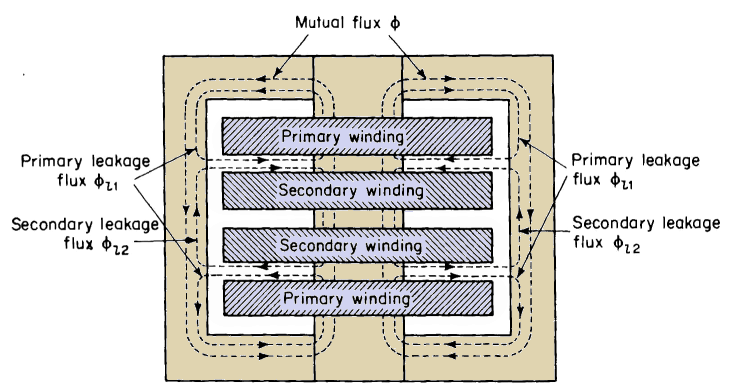
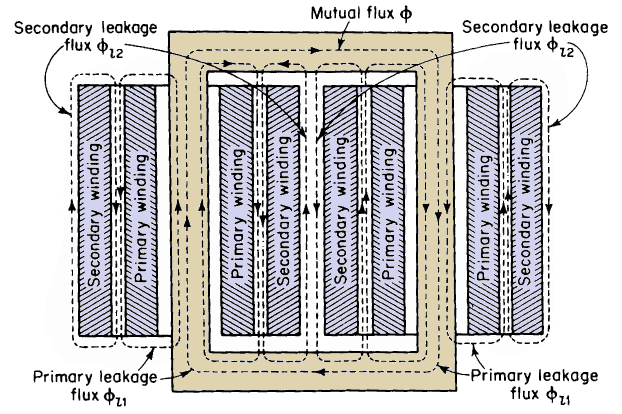
Although Figs. 6-4, 6-7, 6-8, and 6-9 represent iron-core transformers, the magnetic flux in air-core transformers can also be divided into the three components, namely, mutual flux and primary and secondary leakage fluxes, even though the air-core transformer does not have a discretely defined magnetic core.

The arrangement of the windings shown schematically in Figs, 6-7(a) and 6-7(b) make for high magnetic leakage, since the leakage flux can spread out over a relatively large area. When the windings are arranged as shown in Figs. 6-8 and 6-9, the magnetic leakage is relatively small, since the leakage flux is restricted to paths of relatively small cross sections, and hence, of correspondingly high magnetic reluctance. Although Figs. 6-7, 6-8, and 6-9

Figure 6-9. Winding arrangement in core-type transformer showing approximate paths taken by mutual flux and primary and secondary leakage fluxes.

show separately defined paths for the three component fluxes, these fluxes do not exist as independent entities, but merge into a common flux pattern. Nevertheless, the concept of these three component fluxes facilitates the analysis of transformer performance.

The actual flux paths are such that the leakage fluxes are distributed throughout the windings rather than concentrated into spaces between the windings. As a result, each winding is subjected to partial flux linkages. This means that differing amounts of leakage flux link the different turns of a given winding. Therefore, the leakage fluxes Φ_l1 and Φ_l2 are equivalent leakage fluxes; the former links all N₁ turns of the primary and the latter links all N₂ turns of the secondary. Thus, if λ_l1 = the primary leakage flux linkage, and λ_l2 = the secondary leakage flux linkage, then

[6-29]

and

[6-30]

Furthermore, if Φ is the equivalent mutual flux linking all the turns of both windings, then the total equivalent fluxes linking the primary and the secondary windings, respectively, are

[6-31]

[6-32]

and the primary and secondary terminals voltages are

[6-33]

[6-34]

The primary leakage flux linkage and the secondary leakage flux linkage are

[6-35]

[6-36]

and from these the primary leakage inductance and secondary leakage inductance are, respectively

[6-37]

[6-38]

so that

and

[6-39]

[6-40]

When Eqs. 6-39 and 6-40 are substituted in Eos. 6-33 and 6-34, the primary and secondary voltages are expressed by

[6-41]

[6-42]

Equation 6-42 can be rewritten in terms of i_L on the basis of Eq. 6-15 to read

[6-43]

Since the leakage flux paths are largely in air, the leakage inductances L_l1 and L_l2 are practically constant.

If a sinusoidal voltage, having an effective or rms value of V₁ v, is applied to the primary of an air-core transformer when the secondary is connected to a linear load impedance, the primary current I₁ and the secondary load current I_L will also be sinusoidal. The quantities I₁ and I_L are the rms values of the primary current and secondary load current. It was mentioned in Chapter 5 that the exciting current in iron-core transformers contains harmonics, and is therefore not sinusoidal. The exciting current, however, is small enough in comparison with the rated primary current of the transformer so that its effect on the wave form of the primary and secondary currents is usually negligible in the normal range of load. Thus, if the impedance of the load in the secondary is linear, the primary and secondary currents in an iron-core transformer are practically sinusoidal for normal load conditions if the voltage applied to the primary is sinusoidal. Equations 6-41 and 6-43 can be rewritten in terms of phasor quantities as follows

[6-44]

[6-45]

where

V₁ = the effective applied primary terminal voltage
V₂ = the effective secondary terminal voltage
E₁ = the effective primary voltage induced by the mutual flux
E₂ = the effective secondary voltage induced by the mutual flux
I₁ = the effective primary current
I_L = the effective secondary load current
R₁ = the resistance of the primary winding
R₂ = the resistance of the secondary winding
X_l1 = 2πfL_l1 = the primary leakage reactance
X_l2 = 2πfL_l2 = the secondary leakage reactance
f = the frequency in cycles per second