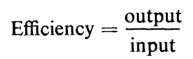Capacitors, Magnetic Circuits, and Transformers is a free introductory textbook on the physics of capacitors, coils, and transformers. See the editorial for more information....

Home The Transformer Transformer Losses and Efficiency
 
del.icio.us Reddit Facebook StumbleUpon MySpace Twitter Search the VIAS Library  |  Index

Transformer Losses and Efficiency

The losses in a transformer are the core loss due to hysteresis and eddy currents in the core, as explained in Chapter 5; and the copper losses in the windings and stray losses due to eddy currents induced by the leakage fluxes in the tank and other parts of the structure. The sum of the copper losses and the stray losses is known as load losses and is determined from the short-circuit test, being I2Req The core loss is determined from the open-circuit test.

The power efficiency of a device is the ratio of the useful power output to the power input, the power input being equal to the useful power output plus the power losses. Thus

[6-58]

[6-59]

The rated load efficiency of transformers is generally quite high (as high as 90 percent for transformers, as small as 1 kva) and since the losses can be determined readily, Eq. 6-59 is preferred to Eq. 6-58 for calculations of efficiency for reasons of accuracy.

Methods of testing transformers and of calculating their performance have been developed to a high degree and are specified in the ASA Standards. These include corrections for temperature and other refinements that are not within the scope of this text.

Example 6-5a: Determine the efficiency of the transformer in Examples 6-2, 6-3, and 6-4

(a) At rated load 0.80 power factor.

(b) At one-half rated load 0.60 power factor.

 
Solution: It is important to note that the transformer delivers rated load when it

delivers its rating, at rated voltage, in volt-amperes, regardless of power factor.

(a) Output = 150000 x 0.80 = 120000 w

Rated current = 62.5 amp (on the high-voltage side)

The equivalent resistance of the transformer referred to the high-voltage side from Example 6-4 is

Req1 = 0.425 ohm

and the load loss at rated current is

I21Req1 = (62.5)2 x 0.425 = 1660 w

which is also the value measured in the short-circuit test at rated current.

The no-load loss at rated voltage is from Example 6-3

Poc = 580 w

The total loss then is 1660 + 580 = 2240 w and the power input
= output + losses
= 120000 + 2240
= 122240 w

The rated-load efficiency at 0.80 power factor is therefore

(b) One-half rated load = 150000 x 1/2 = 75000 va

Output = 75000 x 0.60 = 45000 w

The core loss is assumed to remain unchanged as the secondary voltage is again at rated value. Hence

Poc=580w

The load losses, however, vary as the square of the current and, therefore, at one-half rated current, are equal to one-fourth the load losses at full-load current. Hence

I2Req = 1/4 x 1660 = 415w

and the total losses are 580 + 415 = 995 w. The efficiency, then, at one-half rated load 0.60 power factor, is

A power transformer may undergo a considerable variation in load during a 24-hr period. There may be intervals during which the transformer carries a substantially rated load and others during which the transformer carries only a small part of its rating. So if the efficiency of operation is to be taken over such a 24-hr period, the energy efficiency is the proper criterion. The energy efficiency for a given period is the ratio of the kilowatt-hour output to the kilowatt-hour input and depends not only on the characteristics of the transformer but also on the load cycle.

For instance, to compute the energy efficiency for a 24-hr period, or the all-day efficiency, it is necessary to integrate the core loss and the load losses over a 24-hr period. The core losses are practically constant since the voltage of a power transformer is nearly constant. The energy in kilowatt hours associated with the core loss is merely the product of the core loss in kilowatts and the time in hours during which the transformer is energized. It is more difficult to compute the energy loss due to the load losses (I2R) when the load is fluctuating. However, if the daily load schedule is known and minor fluctuations of the load can be neglected, the load curve can be approximated by a step curve, and the energy losses can be calculated for a 24-hr period as shown in Example 6-5 below.

Example 6-5b: The load schedule for a 24-hr period on a 30-kva, 2400/240 v, 60-cycle transformer is as follows

Hours Kw PF
10 2.5 0.75
8 12.5 0.80
3 20.0 0.85
3 25.0 0.90

The data taken from open-circuit and short-circuit tests follow

High side open, measurements on low-voltage side
240 Volts
2.45 Amperes
154 Watts
Side short circuited, measurements on high side
61.1 Volts
12.5 Amperes
706 Watts

Determine the energy efficiency for a daily load cycle.

 
Solution: The core losses are constant for the 24-hr period, and the energy dissipated

in core loss is therefore

(154 x 24)/1000 = 3.70 kwhr

The load losses are proportional to the square of the current, i.e., to the square of the kva load and the energy dissipated in the load loss are computed in the following table.

Hours Kw Kwhr PF Kva Load loss Kw Load loss Kwhr
10 2.5 25 0.75 3.33 0.00871 0.087
8 12.5 100 0.80 15.63 0.192 1.536
3 20.0 60 0.85 23.50 0.433 1.299
3 25.0 75 0.90 27.80 0.606 1.818

The load loss is proportional to the square of the kva load; hence, at 3.33 kva, the load loss is

and for 15.63 kva

Total output = 260 kwhr
Total load loss = 4.74 kwhr
Total core loss = 3.70 kwhr
Input = 268.44 kwhr

 

Home The Transformer Transformer Losses and Efficiency

Last Update: 2011-02-16