A common misunderstanding of regression occurs if the correlation between two variables is near zero and the ratio of the ranges of the x- and the y-scale is so high (or low) that the data appears to lie on the regression line. However, changing the scale of the y-axis to the same range as the x-axis immediately shows that the data is in fact only weakly correlated.

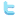
As the goodness of fit (or coefficient of determination) is equal to the square of the correlation coefficient, it will be around zero, despite the regression line seems to fit the data fairly well (if the scales of the axes are too different).

At the left you see an example showing a small goodness of fit due to weakly correlated data. When calculating both the direct regression model (red line) and the inversion model (blue) line one can immediately see that they differ quite a lot (which indicates a poor fit of the regression model).

Download
English version	[319 kB]
German version	[319 kB]
After downloading please unpack all files of the zipped packages and start the executable.

The program Regrot allows to decorrelate data by rotating a data set around the origin. The corresponding regression models (both the direct and the inverse model) are calculated and displayed. These models differ most when the correlation between x and y approaches zero.