Linear regression can be seen as kind of an optimization problem: if the regression line is displayed in the space spanned by the parameters of the equation of the regression line, we can easily find the solution.

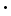Assuming that the line is defined by y = kx + d we can display this line by a single point in the {k,d} space. If we augment this 2-dimensional space by a third coordinate which represents the sum of the squared residuals we finally arrive at a three dimensional surface, which is commonly called the error surface of the regression problem. The optimum line (the "regression line") can now be found by searching the minimum of the error surface.

Download
English version	[334 kB]
German version	[334 kB]
After downloading please unpack all files of the zipped packages and start the executable.

This program has been written to explore the relationship between the data points and the error surface of the regression problem. On one hand you can learn how to represent a line in two different spaces ({x,y} and {k,d}), and on the other hand you see that solving the regression problem is nothing else than finding the minimum in the error surface.