Share this Page:






|
Learning by Simulations focuses on math, physics, computer sciences and chemistry. Following is a short overview on the topics covered by the simulation programs.
|
Mathematics |
Principal Component Analysis, Fourier Synthesis, Travelling Salesman Problem, Vector Fields, Sampling Theorem, Splines, AD Conversion, Riemann Sum, Random Number Generators, Tangent and First Derivative, Function Plotter, ... |
Statistics |
Central Limit Theorem, Distribution Calculator, Leverage Effect in Regression, Error Surface of Linear Regression, Correlation Coefficient, Regression and Weakly Correlated Data, Time Averaging of Signals, Discrete Distributions, Linear Regression for Chemical Analysis, Measures of Location, Cauchy Distribution... |
Computer
Sciences |
Number systems (binary, octal, decimal, hexadecimal), ASCII Encoding, RGB Color Mixing, Direct Sequence CDMA, ... |
Physics |
Electron Multiplier, Radiation of a Blackbody, Varactor Diode, Electric Field Lines, Coupled Radiators, Ion Optics, Gravitational Energy, Optical Lens, Array Antennas, Damped Resonator, ... |
Chemistry |
Mass Spectrometer, Molecular Formulas, Atomic Spectra, Sector Field Mass Spectrometer, Overlapping Chromatographic Peaks, Acid-Base Titration, Calculation of Molecular Weight, Polyprotic Acids, ... |
|
We plan to publish, on the average, one interactive learning tool every few weeks, finally arriving at about 100 simulations which will be available for download from this site. So come back in regular intervals and check if there's something new which fits your needs.
Recently Published:
Principal Components
[Jul-14, 2012] |
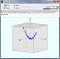 |
Shows the relationship between Cartesian coordinates and principal components.
|
Cauchy Distribution
[Oct-31, 2010] |
 |
Shows the features of Cauchy distributed data and the non-existence of the expectation value.
|
Damped RLC Circuit
[Aug-05, 2010] |
 |
Shows the behavior of an RLC circuit.
|
Polyprotic Acids
[Feb-27, 2008] |
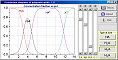 |
Calculates the distribution of dissociated ions of polyprotic acids.
|
Measures of Location
[Oct-04, 2007] |
 |
Shows the stability of the mean, median, and mode of a distribution.
|
|
|

 Overview
Overview