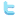
A vector field is a field which associates a vector to every point in the field space. Vector fields are often used in physics to model observations which include a direction for each point of the observed space. Examples are movement of a fluid, or the force generated by a magnetic of gravitational field, or atmospheric models, where both the strength (speed) and the direction of winds are recorded.

The effect of vector fields can be easily calculated by applying difference equations to all points of the observed space. Thus the state of each point of the space R at the time T+1 is calculated by applying the difference equation to each point at the time T. For example, using the two equations x_t+1 = x_t - y_t and y_t+1 = y_t + x_t will result in a rotation of the points in a two-dimensional space. Another transformation which creates two vortices is shown in the screen shot below:

Download
English version	[333 kB]
German version	[333 kB]
After downloading please unpack all files of the zipped packages and start the executable.

The program VectorFields allows to define almost arbitrary difference equations and to apply them to a cloud of random points in a two-dimensional space. In order to get a quick impression of the power of the vector field calculus, a few basic vector field transformations are predefined and can be selected from the selection box at the top right. For downloading the program click the floppy disk symbols at right.