You are working with the text-only light edition of "H.Lohninger: Teach/Me Data Analysis, Springer-Verlag, Berlin-New York-Tokyo, 1999. ISBN 3-540-14743-8". Click here for further information.

Table of Contents Multivariate Data Modeling MLR Estimation of New Observations
Index
See also: MLR, ANOVA 

MLR
Estimation of New Observations

When calculating the regression parameters ai of the general multiple linear regression equation

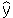one is not only interested in the actual parameters ai but also in an estimate of the confidence interval of both the parameters ai and the estimated target variable . While estimating the standard deviation of the parameters is quite simple, the estimation of the standard deviation of 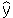is rather complicated. The reason for this is that the distribution of 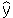depends on the particular set of ai. In general, the multivariate distribution function of 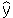can be rather complex.

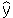However, there are two ways to estimate the standard deviation of , the first being rather easy to implement, the second one is more demanding:

Rough Approximation: We can use the standard deviation s of the residuals to estimate the standard deviation of future values of y, i.e. 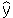. The interval of 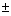2s can be interpreted as a rough approximation to the accuracy of the model (that is, the accuracy with which the model will predict future values of y for particular values of xi). The calculation of s is easy and straightforward:

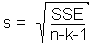
with SSE being the sum of squared residuals, n being the number of observations, and k being the number of independent variables.

Exact Solution: The exact way to calculate the confidence interval of 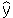can be seen as an extension of the Working-Hotelling confidence band of simple regression. In the case of multiple linear regression this band becomes a k-dimensional volume. The estimated value 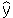falls within the (1-a) confidence interval:

with s being the standard deviation of the residuals, c being the augmented vector of the x-values, (XTX)-1 being the inverse covariance matrix, and ta/2 being the quantile of the t-distribution at the probability a/2.

Last Update: 2006-Jän-17