 You are working with the text-only light edition of "H.Lohninger: Teach/Me Data Analysis, Springer-Verlag, Berlin-New York-Tokyo, 1999. ISBN 3-540-14743-8". Click here for further information.
You are working with the text-only light edition of "H.Lohninger: Teach/Me Data Analysis, Springer-Verlag, Berlin-New York-Tokyo, 1999. ISBN 3-540-14743-8". Click here for further information.
 You are working with the text-only light edition of "H.Lohninger: Teach/Me Data Analysis, Springer-Verlag, Berlin-New York-Tokyo, 1999. ISBN 3-540-14743-8". Click here for further information. You are working with the text-only light edition of "H.Lohninger: Teach/Me Data Analysis, Springer-Verlag, Berlin-New York-Tokyo, 1999. ISBN 3-540-14743-8". Click here for further information.
|
Table of Contents  Statistical Tests Statistical Tests  Comparing Variances Comparing Variances  Two-Sample F-Test Two-Sample F-Test |
|
| See also: one-sample chi-square test, F-distribution, survey on statistical tests |   |

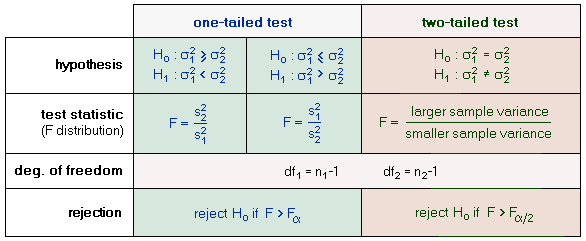
Remarks:
Example:
Suppose you have two series of measurements, one with 10 observations,
and one with 13 observations. The variance of the first series is 0.88,
and the variance of the second series is 1.79. Is the variance of the second
series significantly larger than the variance of the first series (at a
significance level of 0.05)?
In order to check this, we assume the null hypothesis that the variance
of the second series is not larger than the variance of the first
series. The alternative hypothesis would be that the second variance is
indeed larger than the first one. Next we have to calculate the F statistic:
F = 1.79/0.88 = 2.034. Now we can compare the F statistic with the critical
value at a 5 percent level of significance. By using the distribution
calculator we find a critical value of 3.073. Since F is only 2.034
we cannot reject our null hypothesis (the second variance is not significantly
larger than the first one).
Last Update: 2005-Jul-16