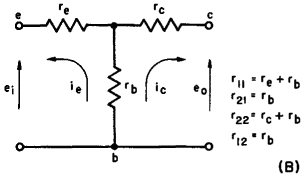
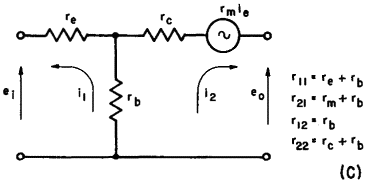
Equivalent Active 'T' Network

Author: Leonard Krugman

While the passive network serves as an interesting introduction to transistor analysis, it does not describe this device completely, because the transistor is known to be an active network. The equivalent circuit of the transistor can be represented in a number of ways; the most widely used configuration is illustrated in Fig. 3-7 (C). The basic difference between the equivalent circuits representing the active network and the passive network is the voltage source e = r_mi_e inserted in the collector arm. In general, the passive network determines three of the characteristics of the active network. In the case under consideration, the input resistance r₁₁, the output resistance r₂₂, and the backward transfer resistance r₁₂ are the same for the passive and active networks shown in Figs. 3-7 (B) and 3-7 (C). The only difference is the value of the forward transfer resistance r₂₁, which in the case of the passive network equals r_b, and in the active network equals r_m + r_b.

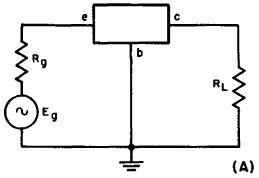
Fig. 3-7. (A) The basic circuit for transistor four-terminal network analysis.
(B) Transistor equivalent "T" on a passive basis.
(C) Transistor equivalent "T" on an active basis.

, the equations for an active network under ideal conditions (that is, when the resistance of the signal source is zero, and the resistance of the load is infinite) become:

r₁₁ = r_e + r_b

r₁₂ = r_b

r₂₁ = r_b + r_m

r₂₂ = r_c + r_b

The four parameters in this active network are the emitter resistance r_e, the base resistance r_b, the collector resistance r_c, and the voltage source r_mi_e. The parameter r_m is represented as a resistance since it acts as the proportionality constant between the input emitter current and the resulting voltage source in the collector arm. The mathematical logic of the resistance r_m is easily derived as follows: In preceding chapters, the current gain α was defined as the ratio of the resulting change in collector current to a change in emitter current, α = i_c/i_e. The equivalent voltage introduced into the collector circuit is e = i_cr_c. Since i_c = αi_e, e = αi_er_c. Since α is a dimensionless parameter, it can be related to the collector resistance by a resistance parameter r_m. Thus, α = r_m/r_c. Substituting this latter equality, e = αi_er_c = r_m/r_ci_er_c = r_mi_e.

There is no phase inversion in the grounded base connection; a positive signal applied to the emitter produces an amplified positive signal of the same phase at the collector.