| General Chemistry is a free introductory textbook on chemistry. See the editorial for more information.... |

|

Home  Atoms Atoms  The Structure of an Atom The Structure of an Atom  Ionization Energies of the Atoms Ionization Energies of the Atoms |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||






|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Ionization Energies of the AtomsAuthor: John Hutchinson
Each electron must move about the nucleus in an electrical field generated by the positive charge of the nucleus and the negative charges of the other electrons. Coulomb's law determines the potential energy of attraction of each electron to the nucleus:
where +Ze is the charge on the nucleus with atomic number Z and -e is the charge on the electron, and r is the distance from the electron to the nucleus. We can directly measure how much energy is required to remove an electron from an atom. Without concerning ourselves with how this measurement is made, we simply measure the minimum amount of energy required to carry out the following "ionization reaction":
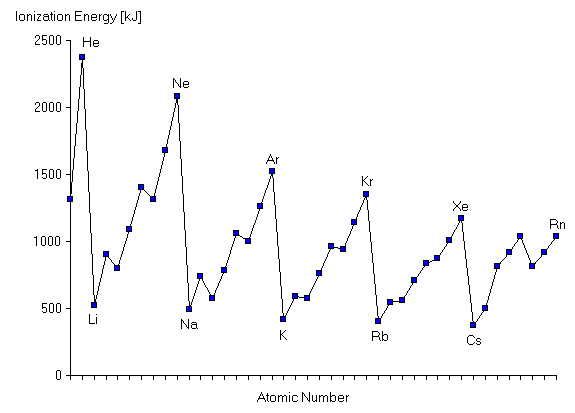
Here, A is an atom in the gas phase, and A+ is the same atom with one electron e-removed and is thus an ion. The minimum energy required to perform the ionization is called the ionization energy. The values of the ionization energy for each atom in Groups I through VIII of the periodic table are shown as a function of the atomic number here.
This figure is very reminiscent of the Periodic Law, which states that chemical and physical properties of the elements are periodic functions of the atomic number. Notice that the elements with the largest ionization energies (in other words, the most tightly bound electrons) are the inert gases. By contrast, the alkali metals are the elements with the smallest ionization energies. In a single period of the periodic table, between each alkali metal atom and the next inert gas atom, the ionization energy rises fairly steadily, falling dramatically from the inert gas to the following alkali metal at the start of the next period. We need a model which accounts for these variations in the ionization energy. A reasonable assumption from Coulomb's law is that these variations are due to variations in the nuclear charge (atomic number) and in the distance of the electrons from the nucleus. To begin, we can make a very crude approximation that the ionization energy is just the negative of this attractive potential energy given by Coulomb's law. This is crude because we have ignored the kinetic energy and because each electron may not have fixed value of r. Nevertheless, this approximation gives a way to analyze this figure. For example, from Coulomb's law it seems to make sense that the ionization energy should increase with increasing atomic number. It is easier to remove an electron from lithium than from neon because the nuclear charge in lithium is much smaller than in Neon. But this cannot be the whole picture, because this argument would imply that sodium atoms should have greater ionization energy than Neon atoms, when in fact sodium atoms have a very much lower ionization energy. Similarly, although the ionization energy rises as we go from sodium to argon, the ionization energy of Argon is still less than that of Neon, even though the nuclear charge in an Argon atom is much greater than the nuclear charge in a Neon atom. What have we omitted from our analysis? The answer is that we must consider also the distance of the electrons from the nucleus. Since it requires much less energy to ionize a sodium atom than to ionize a Neon atom even though sodium's nuclear charge is greater, it must be that the electron which we remove from a sodium atom is much farther from the nucleus than the electron in the Neon atom. We can make the same comparison of the electrons removed during ionization of Neon and Argon atoms: the Argon electron must be farther from the nucleus than the Neon electron. On the other hand, since the ionization energy fairly smoothly increases as we move from lithium to neon in the second period of elements, this reveals that the electrons are increasingly attracted to the nucleus for greater nuclear charge and suggests that the electrons' distance from the nucleus might not be varying too greatly over the course of a single period of the table. If we follow this reasoning, we can even estimate how far an electron might typically be from the nucleus by using our crude approximation that the ionization energy is equal to the negative of the Coulomb potential and solving for r for each atom. This gives an estimate of distance of the electron from the nucleus:
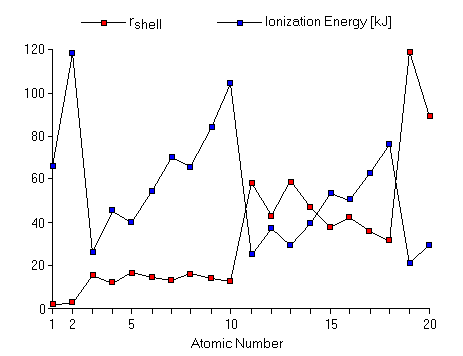
Values of rshell calculated in this way are shown for the first 20 elements here. Also shown for comparison is the ionization energy for these elements. Notice that the approximate distance of the electrons from the nucleus increases in steps exactly coinciding with the increases and dips in the ionization energy.
Although these distances we have calculated do not have a precise physical meaning, this figure suggests a significant conclusion. The electrons in the elements are arranged into "shells" of increasingly greater distance from the nucleus. Hydrogen and helium, with one and two electrons, have ionization energies consistent with electrons at similar and close distance from the nucleus. Then the second row elements lithium through neon have virtually identical sizes, though larger than that for the first two elements. The third row elements, sodium argon, have an approximate electron-nuclear distance which fluctuates a bit but is consistently larger than the second row elements. Because the sizes of the atoms appear to grow in steps which correspond exactly to the periods of the Periodic Table, it seems that the electrons in the atoms are grouped into sets which are differing distances away from the nucleus. The first two electrons, as in Helium, are close to the nucleus, whereas additional electrons, as in lithium to neon, are farther from the nucleus than the first two. The suggests that, for atoms lithium to neon, the first two electrons are in an inner "shell", and the remaining electrons are in an outer "shell." We can refine this shell model for the electrons in an atom with further analysis of ionization energies. We can remove any number of electrons in sequence, forming ions with greater charge. We have been examining the first ionization energy,IE1, but each successively removed electron has successively greater ionization energy: First ionization energy IE1:
Second ionization energy IE2:
Third ionization energy IE3:
The sequential ionization energies for the elements in the second row of the periodic table are shown here. Successive Ionization Energies (kJ/mol)
Note that the second ionization energy is always greater than the first, and the third is always greater than the second, etc. This makes sense, since an electron should be more strongly attracted to a positively charged atom than to a neutral atom. However, the data in the table show a surprising feature. In most cases, the ionization energy increases a fairly large amount for successive ionizations. But for each atom, there is one much larger increase in ionization in the sequence. In Na for example, IE2 is nearly 10 times greater than IE1. Similarly, IE3 is five times greater than IE2 for Mg, although IE2 is less than twice IE1. The data for Na through S all show a single large step in addition to the smaller increases in IE. Looking closely and counting electrons, we see that this unusually large increase always occurs for the ionization where we have already removed all of the outer shell electrons and are now removing an electron from the inner shell. This occurs uniformly across the second row elements, indicating that our shell model is in fact a very accurate predictor of the higher ionization energies. We can now tell how many electrons there are in the outer shell of each atom: it is equal to the number of electrons since the last inert gas. We can conclude that an inner shell is "filled" once we have the number of electrons equal to the number in an inert gas atom. The subsequent electrons are added to a new outer shell. This is commonly referred to as the valence shell of the atom. However, we do not know why only a limited number of electrons can reside in each shell. There is no obvious reason at this point why all the electrons in an atom do not reside in the shell closest to the nucleus. Similarly, there is no reason given for why the number of electrons in an inert gas atom exactly fills the outer shell, without room for even a single additional electron. These questions must be addressed further.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Home  Atoms Atoms  The Structure of an Atom The Structure of an Atom  Ionization Energies of the Atoms Ionization Energies of the Atoms |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Last Update: 2011-02-16


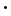 (-e)/r
(-e)/r
 A+(g) + e-(g)
A+(g) + e-(g)