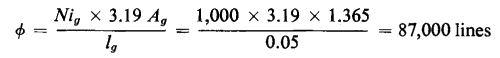Graphical Solution for Simple Magnetic Circuit with Short Air Gap

In simple structures with an air gap, such as that shown in Fig. 3-19, it is a relatively easy matter to determine the mmf for a given value of magnetic flux when leakage can be neglected. For the condition of negligible leakage the flux in the air gap is the same as that in the iron. It is therefore necessary only to compute the mmf for the iron for the given value of flux and the mmf for the air gap at the same value of flux. The sum of these mmf gives the total. However, in the case of a given magnetic structure of iron and air, if the total mmf is given and it is required to determine the magnetic flux, the procedure is not quite as straightforward, since the characteristic of the iron is nonlinear. Nevertheless, such calculations can be facilitated by graphical methods. In one of these the flux vs magnetomotive characteristic is plotted for the iron and the negative air-gap line of flux vs mmf is plotted on the same graph. This is illustrated in Example 3-4.

Example 3-4:

A magnetic structure similar to that shown in Fig. 3-19 is comprised of a steel core with a 0.050-in. air gap. The core is made of laminations 0.014 in. thick. The characteristics of the iron are shown in Fig. 3-11. The core is stacked to a thickness of b = 1.25 in., a width of a = 1.00 in., and the mean length of path = 12 in. There are 600 turns of #14 A.W.G. copper wire; the current is 2.5 amp. Assume a stacking factor of 0.90 for the steel and determine the flux.

Solution:

The flux vs mmf (Φ vs Ni) characteristic is plotted for the iron in Fig. 3-21 on the basis of the magnetization curve of Fig. 3-12 and Mean length of iron = 12.0 in. Ampere turns for iron = 12.0 Hiron Net area of iron =(1.00 x 1.25 x 0.90) - 1.125 sq in. Flux in iron = 1.125 Biron Figure 3-21. Construction for graphical solution of steel core with air gap. Area of air gap corrected for fringing Let Nig = 1,000 amp turns, then Two points are now available to fix the negative air-gap line in Fig. 3-21. The first point is selected at Ni = 1,500 (the total mmf) and Φ = 0, whereas the second has been established at Ni = 1,500 - 1,000 = 500 and Φ = 87,000. The other point at Ni = 500 and Φ = 87,000. The air-gap line in passing through these two points intersects the iron curve at a flux of 101,000 lines. The mmf for the iron then is 330 amp turns; for the air it is 1,500 - 330 or 1,170 amp turns.

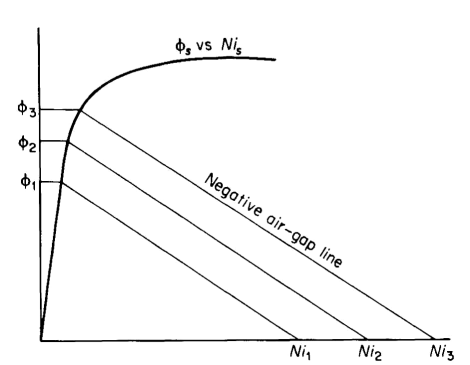
The flux for other values of total mmf can be obtained simply by shifting the air-gap line parallel to itself so that it intersects the desired value of mmf on the abscissa as shown in Fig. 3-22.

Figure 3-22. Construction for graphical solution of steel core with air gap and various mmfs.

Figure 3-23. Construction for graphical solution of steel core with constant mmf for various

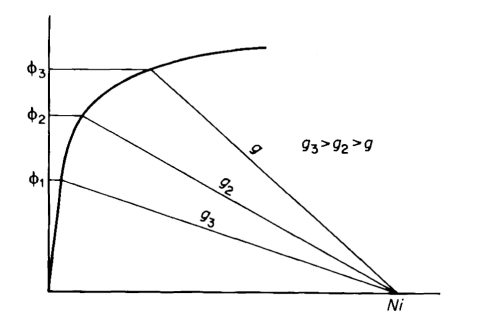
air gap lengths.

On the other hand, if it is desired to determine the flux for a given value of mmf but for various lengths of air gap, the different air-gap lines are drawn from the intersection of the mmf on the abscissa as shown in Fig. 3-23.

Figures 3-22 and 3-23 apply only to fairly simple structures. As magnetic structures become more complex the calculations accordingly become more involved.